Z-Values and P-Values
If we wish to test the statistical significance of an alternative hypothesis, we first have to understand how to calculate the values required for analysis.
First and foremost, our discussion will revolve around a standard normal curve. Z-values and P-values are both inter-related, in which you can calculate one from another.
Z-values on a normal curve measures how many standard deviations a value is away from the mean. On the other hand,
P-values are a probability based on an assumption that H0 is true. It is the area under the curve, and is the smallest significant value where H0 can be rejected.
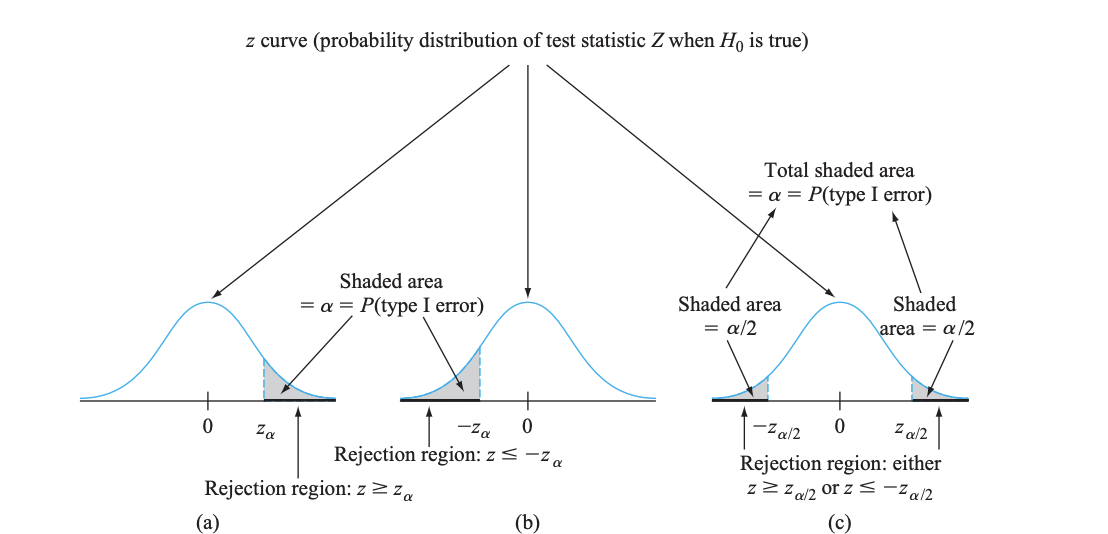
When testing hypotheses, there is a rejection area on each standard normal curve. If the P or Z values fall into this area, then H0 is rejected. So what determines this area? It is based on the significance level, α (alpha). The significance level is essentially the likelihood of incorrectly rejecting H0, which is a type 1 error. The reason why alpha is based on type 1 errors is because they are deemed more serious than type 2 errors. Common significance levels are .10, .05, .01.
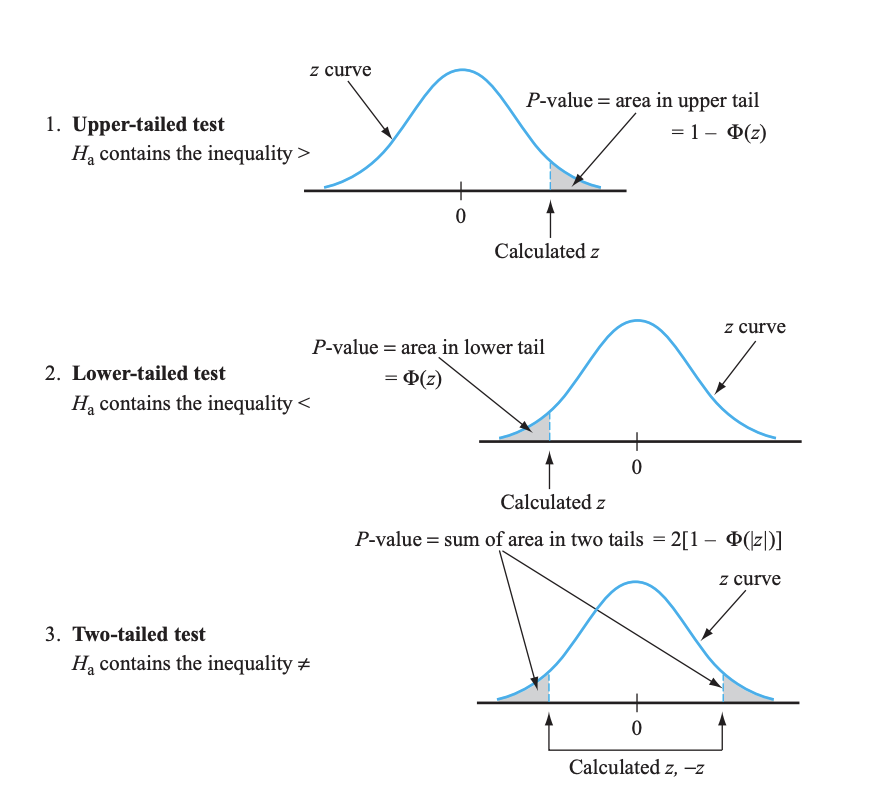
There are three ways alternative hypotheses can be presented: one can state that the sample mean is less than, greater than, or not equal to the mean of the null hypothesis.
Depending on what one is claiming, the rejection region differs. If one claims that the alternative is greater than the alternative hypothesis, the rejection region is in the upper tail. Less than results in the lower tail,
and not equal to results in a two-tailed test, where the rejection region is in both of the tails.