Z value calculations
Calculating the Z-value provides a way to test if the null hypothesis should be rejected or not. On the numerator of the formula shown, we have x̄, which denotes the sample mean, and µ₀ is the mean of the null hypothesis. On the denominator, σ is the known standard deviation, and √n is the square root of the sample size.
Let's do an example. A worker claims that the true temperature for a mechanical system should
operate at 130°F. A sample of n=9 systems were tested, revealing a temperature of 131.08°F. If
the standard deviation is 1.5°F, does the data contradict the worker's claim? Assume a significance level α = .01.
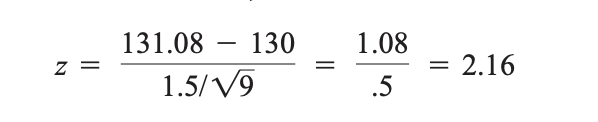The worker is claiming that it does not equal the value, so it is a two-tailed test. The rejection regions are
z.005 and -z.005, where these numbers were obtained by dividing alpha by 2. Alpha/2 is an area, but we want a value from the normal distribution curve. To change this by using a calculator, go to DISTR-->invNorm, and for area, type .005.
This outputs -2.57 and 2.57 for the rejection zone. Now, enter the values from the problem into the formula to calculate the Z-value.
We end up with a z value of 2.16. 2.16 does not fall in the rejection region, so we fail to reject H0.